吴恩达老师有关Deep Learning的第一课—神经网络和深度学习(Nerual Networks and Deep Learning)已经学习结束,在此需要把这次课中需要补充和总结的部分进行整理。
此次的课程一共被分为四周,最开始的一周主要是介绍了神经网络的一些概况,包括有哪些函数以及模型的使用,同时还介绍了简单的使用场景。
到了第二周,最开始就是介绍了二分类(Binary Classification),介绍了逻辑回归(logistic regression),以及前向传播(forward propagation)和反向传播(backward propagation)。在这里学到的第一个技巧就是将数据集按列排列,而不是把数据集按行排列,这样会让整个的实现过程更加简单。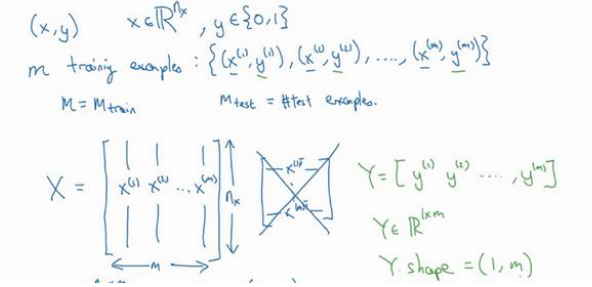
此时的数据集X为Nx行以及m列,Y为1行以及m列。
对于二分类问题,如果你想鉴别一张图片是不是一只猫,那么这个鉴别的结果称为
由于这个符号不易于在博客上表达,以后以yhat作为替代。逻辑回归要做的事情就是得到yhat=wTx+b,但由于这个线性组合可能会很大或很小,但是概率只能在0和1之间,所以此时需要一个东西来限制一下范围,我们称之为激活函数(activation function),最开始介绍的是sigmoid函数,后续还有tanh函数以及ReLU函数,此处不再重复介绍这些函数。介绍完了激活函数接下来对代价函数(cost function)进行了说明,最后学完之后明白了代价函数是在整体上对损失函数(loss function)的表达,所以接下来重点介绍了损失函数。逻辑回归所使用的损失函数是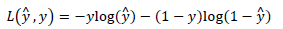
其对应的代价函数是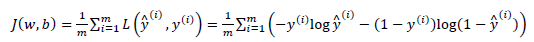
也就是在总体上对参数进行了评估。
为达到代价函数最小的要求,我们采用梯度下降法(Gradient Descent),梯度下降法可以帮助我们调整参数以达到全局最优,以参数w为例,其参数更新公式为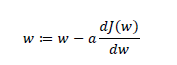
其中a代表了学习率,关于这个值的选定第一门课没有做说明,它主要用来控制步长。而dJ(w)/dw就是函数J(w)对w求导,在代码中使用dw作为表示。而同时考察w和b参数的话,需要使用偏导公式。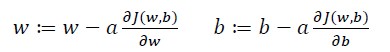
由于此处开始使用到了导数或者说偏导数,所以老师开始讲解导数相关的知识,我们跳过此处的说明。
之后讨论的问题就是逻辑回归中的梯度下降。课程中例子列举了有两个特征,所以此时需要输入参数为w1、w2和b,而这个训练的过程就是不断优化这三个参数,如何进行优化呢?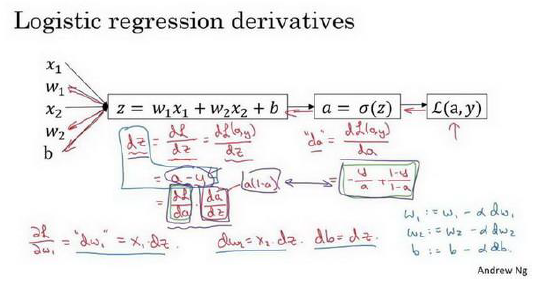
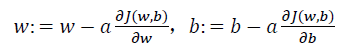
从上面两个图可以知道,我们要更新w和b的值的话就需要求dw和db(单个样本层次,J为整体样本)。从第一张图中我们知道dw1=x1dz,dw2=x2dz,db=dz,那么问题就转换成了求dz,这里的dz就是指dL/dz,就相当于L对z求导,这里利用链式求导法则就能解决,dz=a-y。
结束了这个问题的讨论之后,我们学到了一种新的技术用于提高效率,那就是向量化(Vectorization)。所谓向量化就是将数据集放入一个矩阵中,这样利于python进行矩阵计算,而不需要使用多次循环,导致效率的下降。
第二周的编程作业: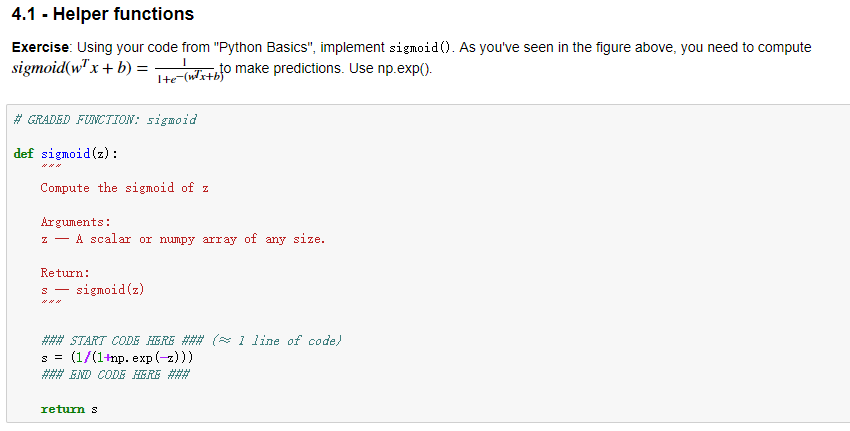
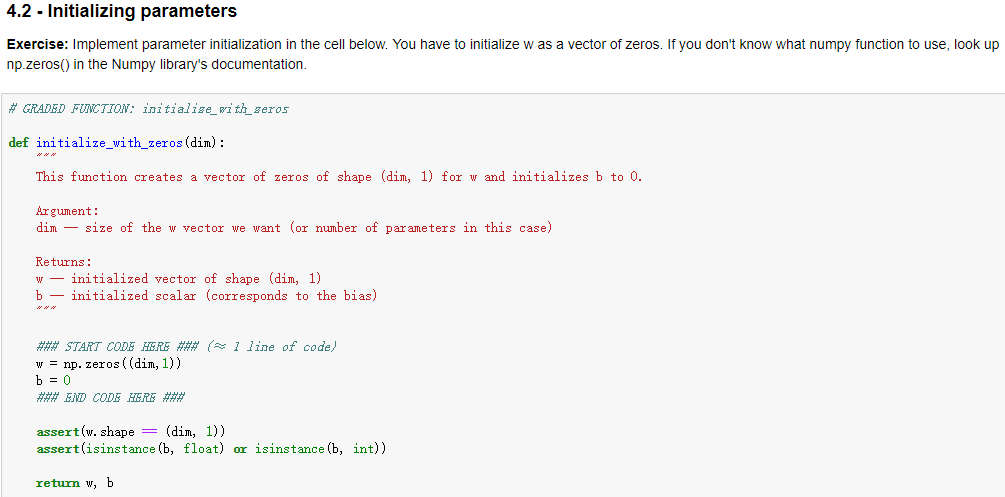
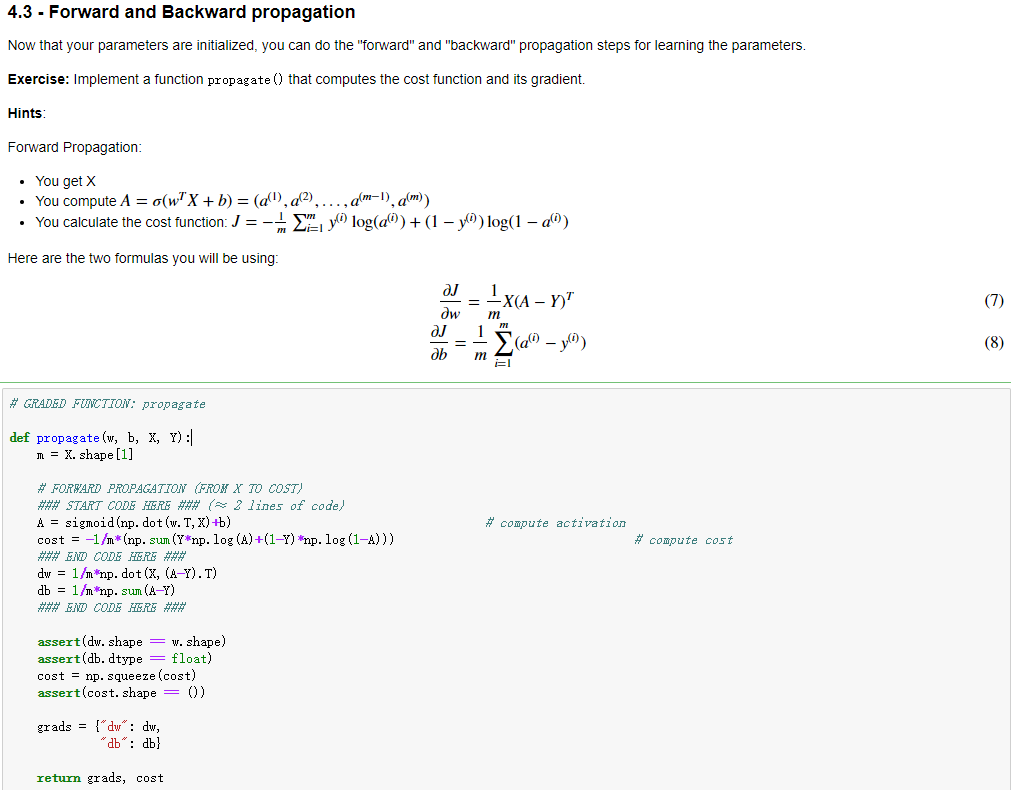
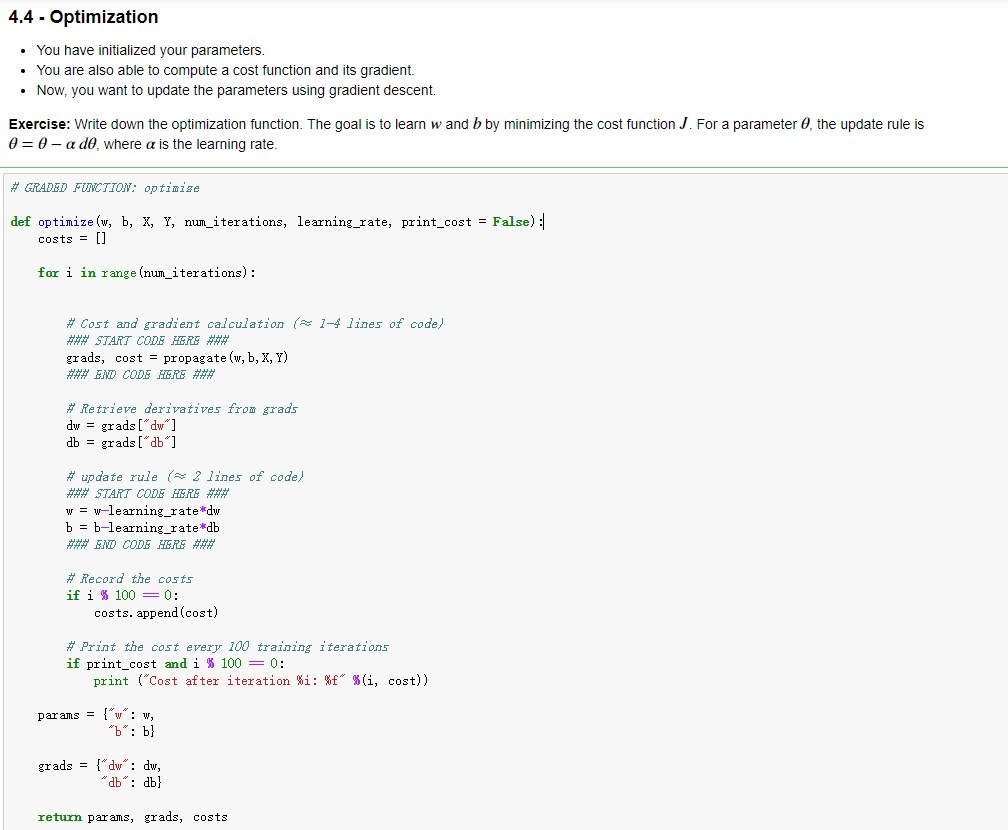
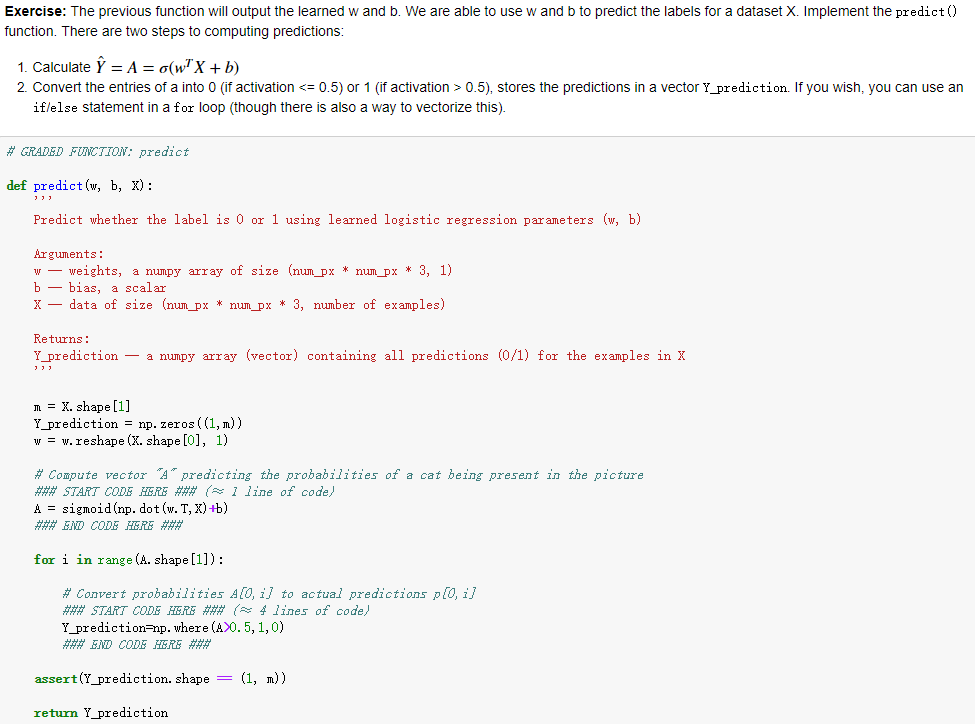
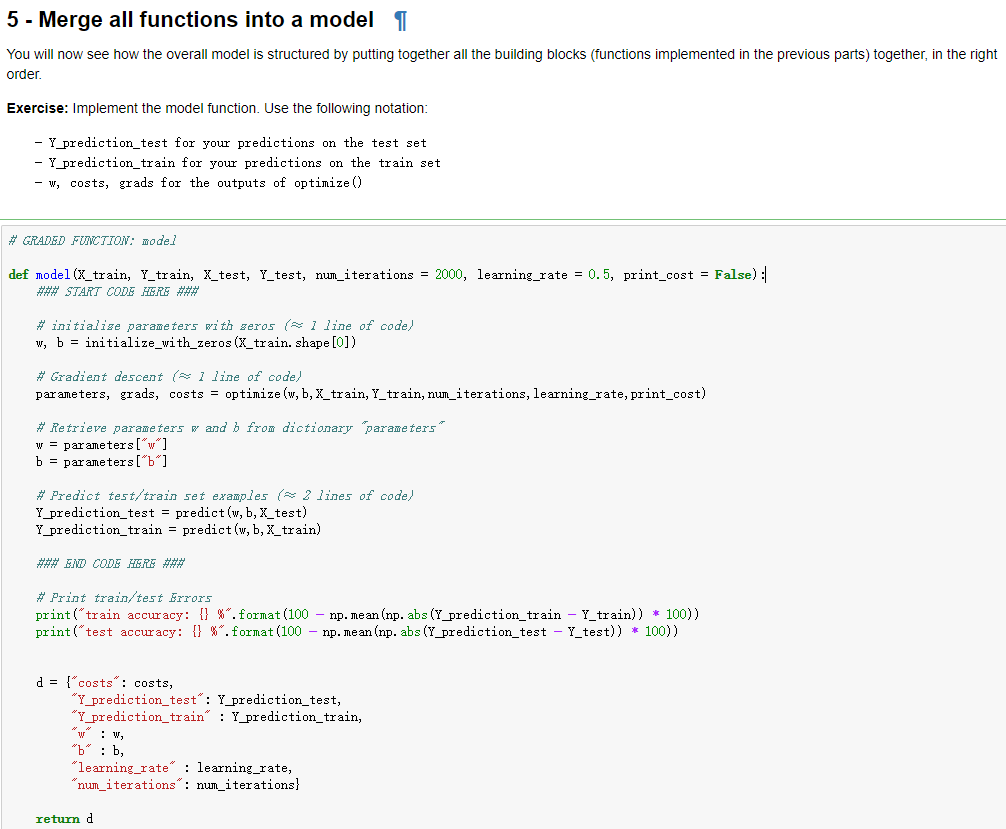
上面这些函数展示一个如何从一个个单独功能的小函数,逐步进行整理,最后融合成了一个model过程。整理一下整个过程,首先实现的是sigmoid函数以及参数w的初始化。之后实现的是前向传播和反向传播中各参数的计算工作,包括A、代价函数以及dw和db。随后就是对参数进行优化了,从grads中取出dw和db,之后就利用之前的w和b的优化公式w=w-αdw以及b=b-αdb进行迭代。然后就是编写了一个预测函数,用于判断经过sigmoid函数计算后的结果矩阵结果是否大于0.5,最后就是将上面的各个函数进行整个,成为一个大model。
结束了第二周的编程工作后,我们就进入了第三周的学习。
第三周一开始介绍了神经网络以及它的表现形式,我们将神经网络分为输入层、隐藏层和输出层。一般来说输入层不算在神经网络的层数统计中,也就是说如果是一个只含有一层隐藏层的神经网络,那么它的层数是2(1个隐藏层加上一个输出层)。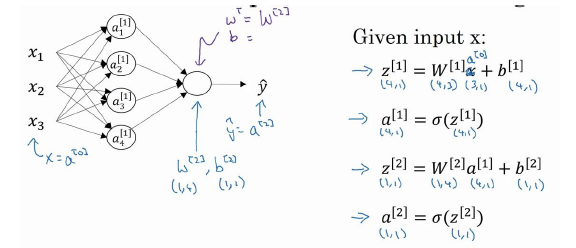
上面这个图就展示了神经网络的计算过程,其中括号中标注的都是当前参数的维度,这一点要特别注意。
上面这个例子明确写明了多样本向量化实现的方式,其中X中的样本是列向量,W1属于矩阵。
说明完上述的矩阵表达后,老师提到了激活函数,介绍了包括sigmoid、tanh、ReLU以及Leaky ReLU。这里主要总结下他们的导数。
Sigmoid: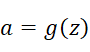
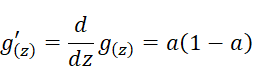
Tanh: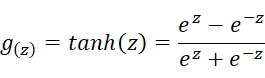
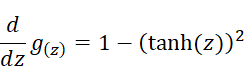
ReLU: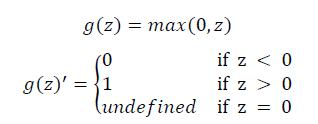
Leaky ReLU: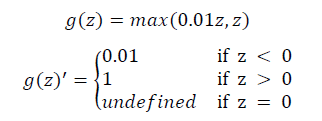
在这周的最后,主要提到了神经网络的梯度下降问题,重新说明了有关前反向传播的方法以及有关初始值的选取。这里我把传播方法放在第四周中进行整理,因为那里讲的更详细。有关初始值的选取,这里就不推荐全0的初始值了,因为如果权重初始化为0,那么隐含单元开始计算同一个函数,所有的隐含单元都会对输出单元有同样的影响,如果初始化为0,那么所有的隐含单元都是对称的,这对梯度下降没有帮助。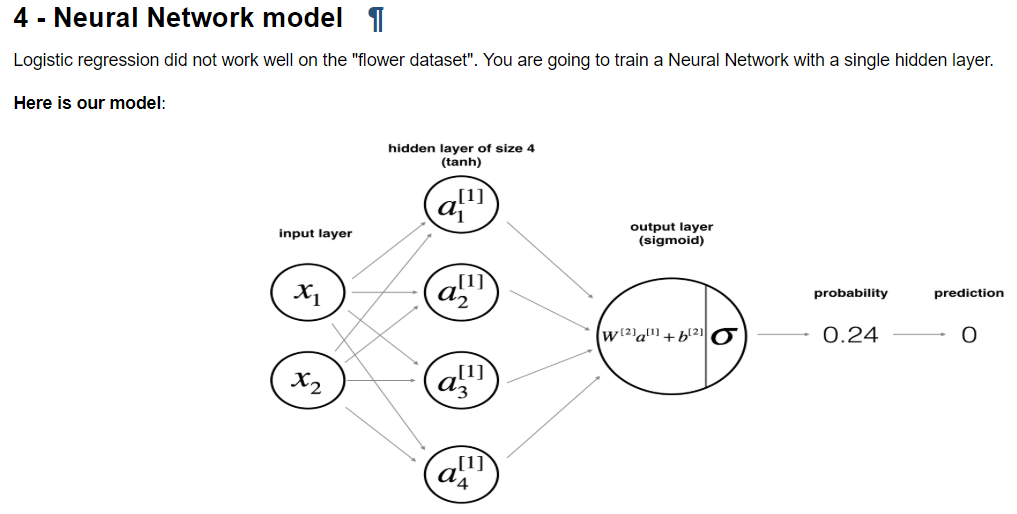

上面两张图展示了本周编程练习所需要的神经网络模型和所涉及到的部分数学公式。
首先是对该神经网络的结构进行设计,此次设计的是包含4个神经元的隐藏层。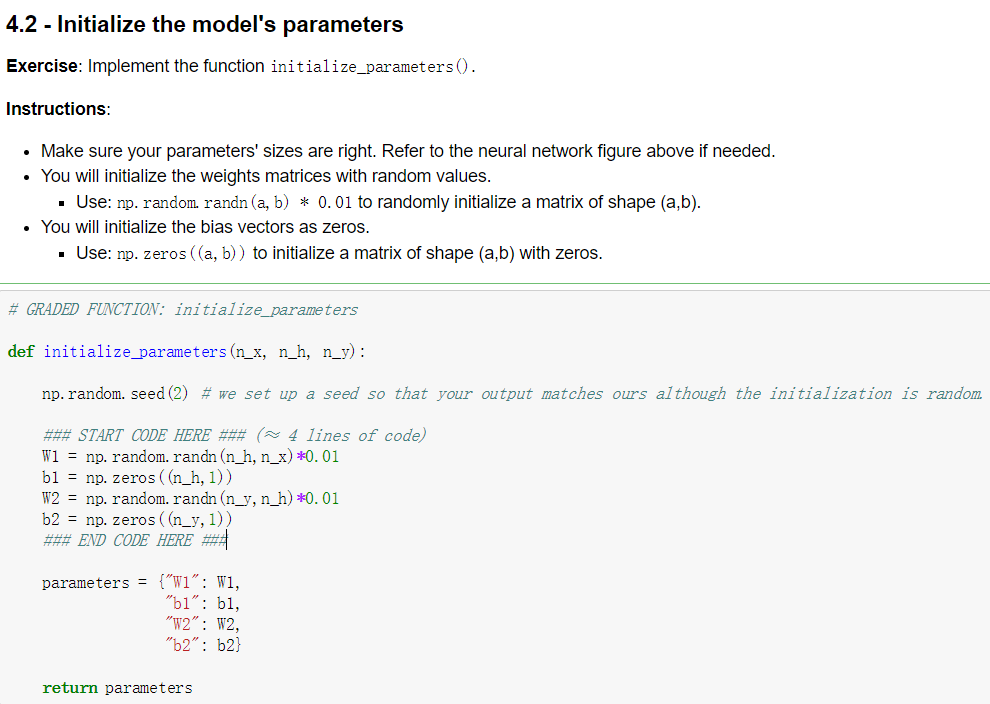
之后就是对需要用到的参数进行设定,包括了系数W以及偏量b。并且由于此次选用了tanh函数,所以w的系数乘上了0.01,并且采用了随机正态分布作为随机初始化变量。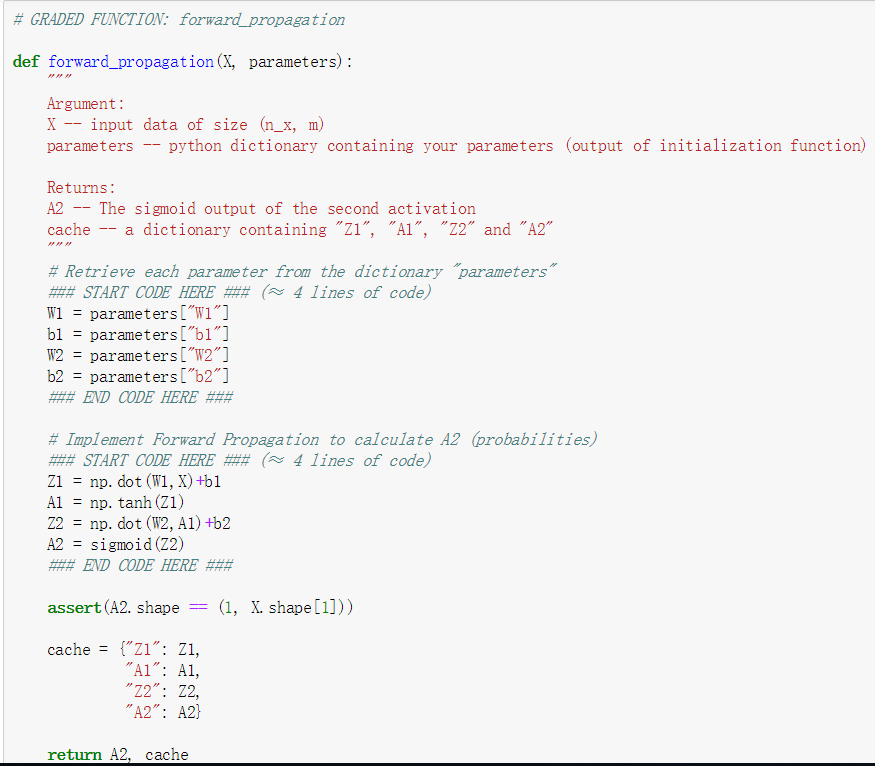
初始化参数之后就开始了前向传播,通过前向传播得到了最后的输出函数。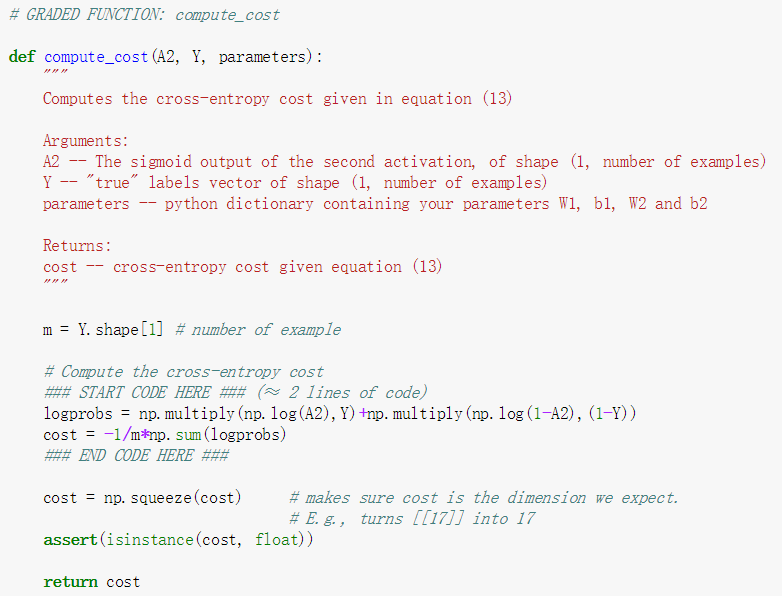
得到输出函数后,就可以进行损失函数的计算。
完成损失函数后,自然就需要进行反向传播,此处给出了反向传播所需要的公式,后续就是对参数进行更新。
最后就是对所有小模块进行整个,得出此次的模型。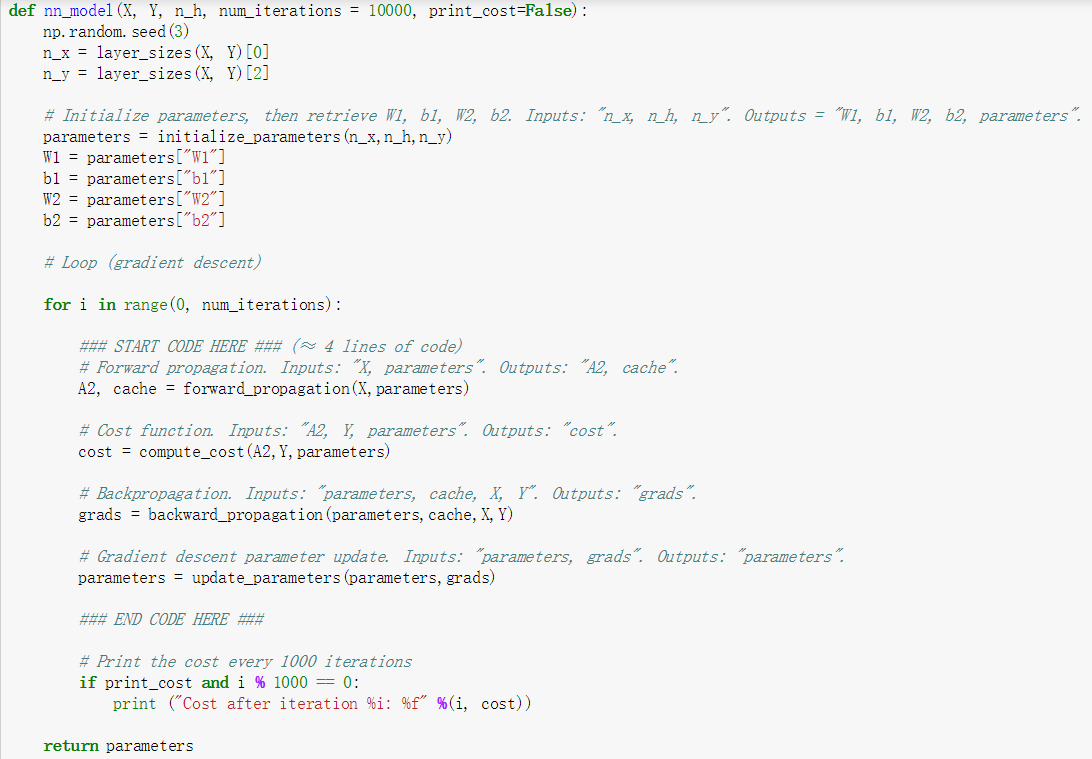
编程练习结束后,我们就进入了第一课最后一周的学习。
最后一周主要是讲了深度神经网络的例子,在之前的学习中,我们一般只使用到了隐藏层为1的神经网络,在这一周我们会学到多层神经网络的相关知识。
在这一周的开始,我们依旧是把重点放在了反向传播上,通过上面的公式就能检查第L层的隐藏层计算是否符合要求。再结合下图能够直观理解神经网络的计算过程,包括前向传播和反向传播。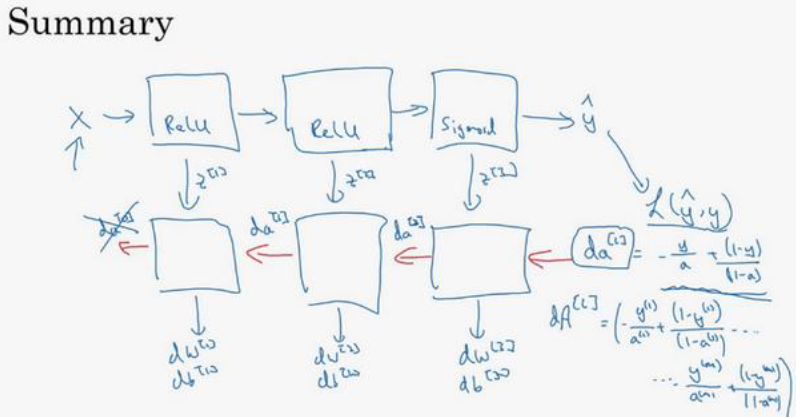
之后提到了维度的检查以及有关参数和超参数的问题,在维度检查时记得使用矩阵之间的关系进行检查,比如如果我们可以知道X和Z的维度,那么就能通过这些维度反推出W和b的维度。而超参数就是指参数的参数,也就是说虽然我们只关注W和b的数值,但是这些数值受到包括但不限于学习率、循环此时、隐藏层等多种因素的影响,所以这些就被称为超参数。
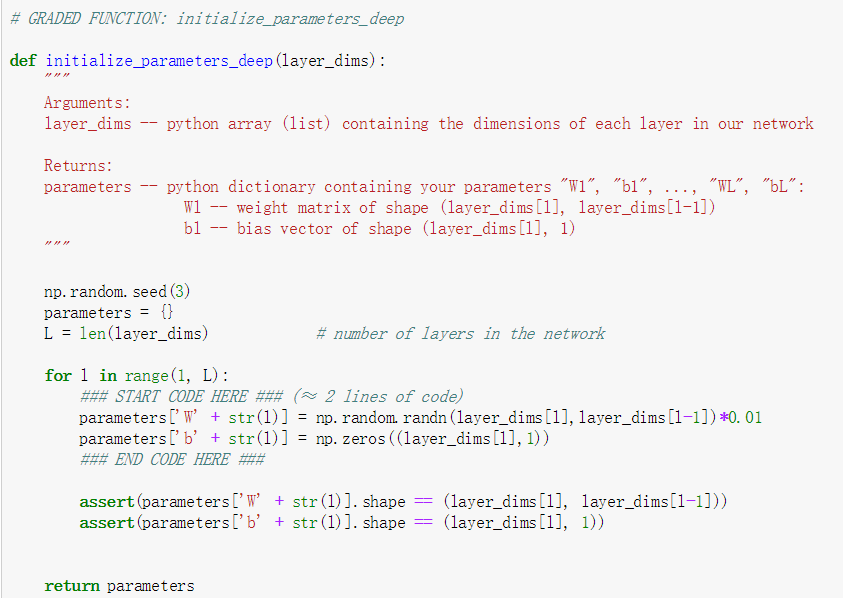

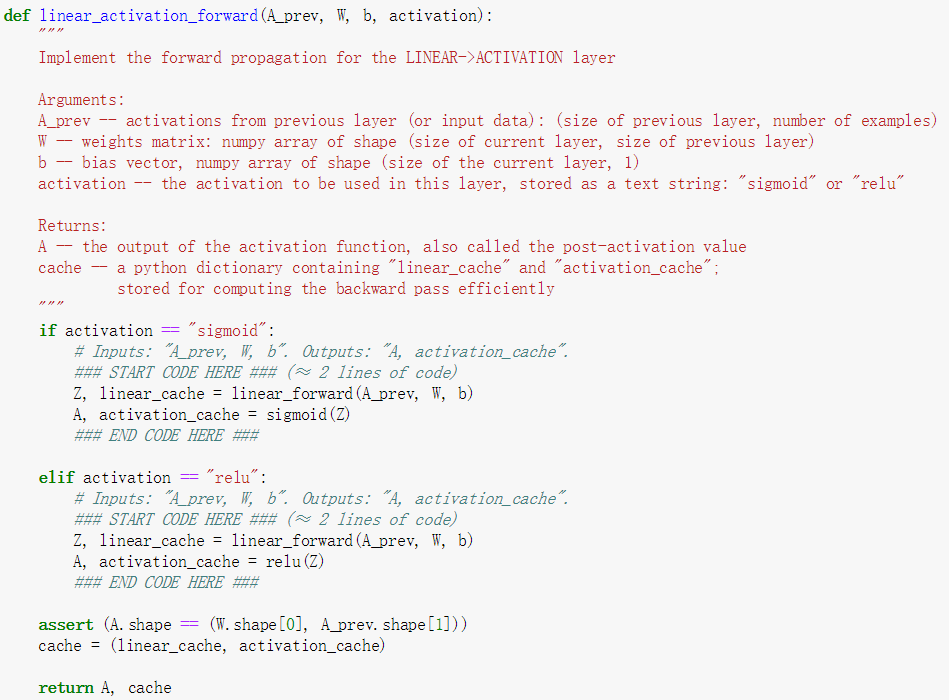
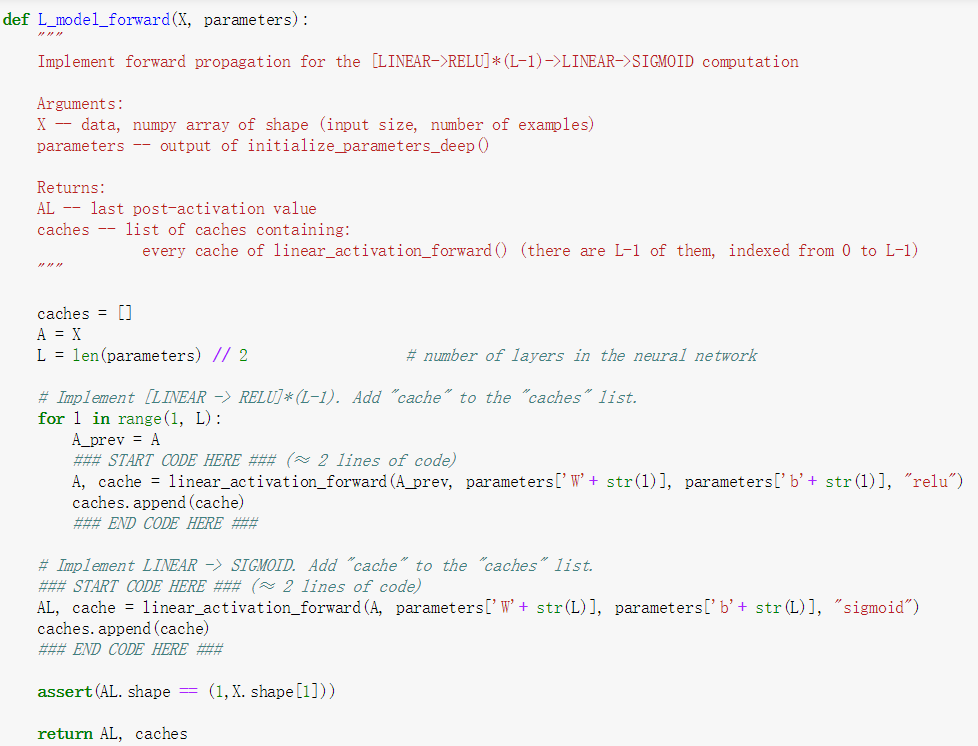

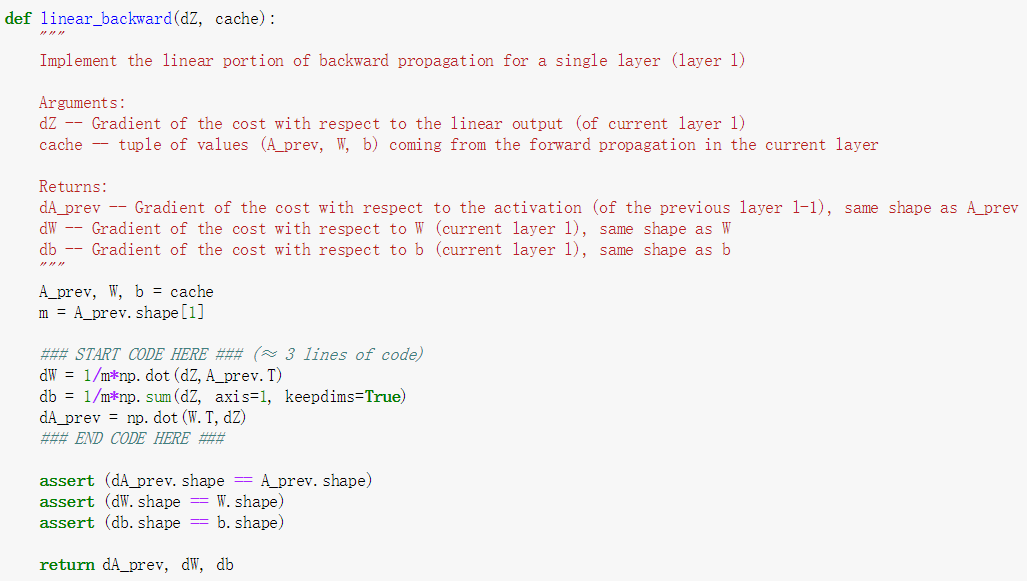
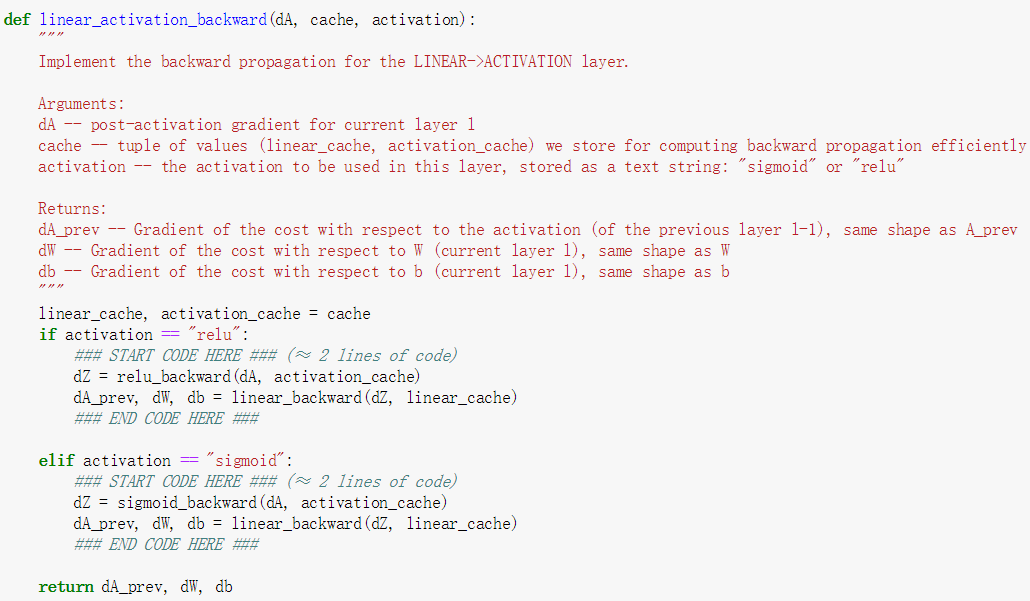
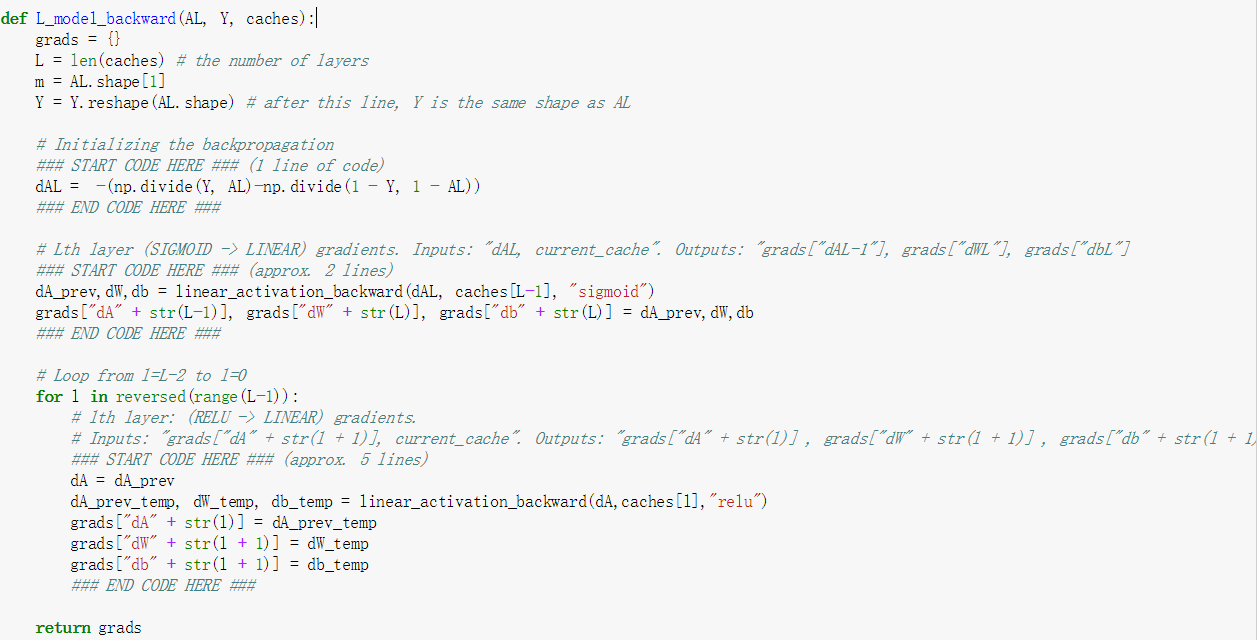
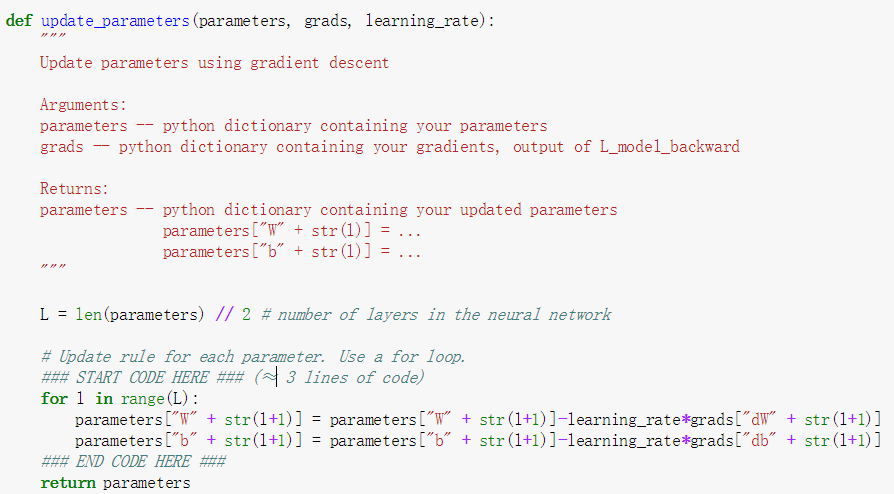
以上的过程已经写过很多遍,只是这次增加了L层,需要使用到循环而已,此时想对整个计算过程做个总结作为这一节课的最后总结。
深度神经网络就是首先定义参数,确定矩阵的维度,然后进行前向传播,传播结束后就是计算损失函数,然后开始反向传播,传播结束后就是更新参数,如此循环,完成最后W和b的确定工作。